
Riccardo Betti
- Robert L. McCrory Professor
- Professor of Mechanical Engineering
- Professor of Physics and Astronomy
- Chief Scientist, Laboratory for Laser Energetics
- Distinguished Scientist, Laboratory for Laser Energetics
- Director, Fusion Science Center of Extreme States of Matter and Fast Ignition
PhD, Massachusetts Institute of Technology, 1992
212 Hopeman
(585) 274-1198
riccardo.betti@rochester.edu
Research Overview
My research concerns the theoretical investigation of the physics of plasmas in thermonuclear regimes. Plasma is the fourth state of matter (solid, liquid, gas and plasma) where high temperatures cause the atoms to decompose into more elementary particles (electrons and ions). Plasmas have a great variety of applications: Fusion energy production (thermonuclear fusion reactors), thermonuclear weapons (H-bombs), X-ray lasers, free electron lasers, magnetohydrodynamic energy conversion (MHD generators), plasma processing, plasma-based radiation sources, high-power microwave generators, beat-wave particle accelerators, astrophysical phenomena and ionospheric physics. Plasma physics generally involves the well known physics of classical mechanics, electromagnetism, and nonrelativistic statistical mechanics. My research is particularly oriented towards the study of thermonuclear plasmas for applications in controlled thermonuclear fusion (magnetic and inertial). More information about my research can also be obtained by visiting the high-energy-density-physics program web page.
Research in Magnetic Confinement Fusion
The primary approach to nuclear fusion has been to design a "magnetic bottle" composed of strong magnetic fields to contain the plasma. Current research in the US is devoted to toroidal magnetic field devices such as tokamaks. In tokamaks, a plasma torus [Fig. 1] is heated by a large current, radio-frequency waves and energetic neutral beams up to a temperature of hundreds of millions of degrees Celsius. At such temperatures, the fusion reaction rate is large enough to produce a significant amount of heating sufficient to sustain the thermonuclear reactions. The heating is generated by the slowing down of the energetic alpha-particles produced in the fusion reactions. When the alpha particle heating balances all the energy losses, the plasma is "ignited".
Figure 1
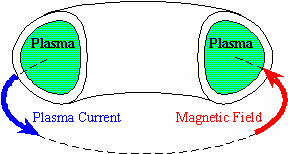
Unfortunately, because of the large pressure and current, the plasma is unstable and hard to confine for a sufficiently long time. The understanding of plasma stability to electromagnetic perturbations is of great importance for the design of the next generation of ignition experiments. Our current research focuses on the kinetic and magnetohydrodynamic stability studies of tokamak plasmas both analytically and numerically.
Research in Inertial Confinement Fusion (ICF)
Edward Teller has noted that inertial confinement fusion (ICF) is essentially the internal combustion engine approach to nuclear fusion energy. ICF schemes are based on the following sequence: (1) a tiny pellet of deuterium-tritium isotopes is injected into a blast chamber, (2) the pellet is compressed to very high densities with an intense laser, (3) the high density and compression heat induces the ignition of the thermonuclear explosion, (4) the kinetic energy carried by reaction products -including neutrons, X-rays, and charged particles- is deposited as heat in a blanket that acts as a heat source in a steam thermal cycle to produce electricity. The ICF combustion engine would use a series of microexplosions to produce power. The application of ICF falls onto several categories such as power production, weapon applications, and fundamental physics. Much of the funding for research activities in this area has been stimulated by the recognition that the environment created by the implosion of a tiny fuel pellet is similar to that of a thermonuclear weapon. Hence, there has been considerable interest in using ICF implosions to simulate thermonuclear weapons after the US ban on nuclear testing.
My research in this area is mainly focused on the hydrodynamic stability of the imploding capsules. The main obstacle in reaching thermonuclear ignition is represented by the onset of so-called "Rayleigh-Taylor instability" (RTI) at the outer and inner surface of the pellet [Fig. 2]. The RTI occurs when a heavy fluid is accelerated against a light fluid. In ICF, the heavy fluid is the compressed target accelerated by the low-density ablating plasma (the light fluid). Because of its devastating effects on ICF implosions (a small perturbation could grow thousands of times during the implosion), it is important to fully understand the physics and the stabilizing mechanisms of such instability. Although the physics of the RTI for two inviscid superimposed fluids is well known, the RTI in laser-accelerated targets is strongly affected by the laser ablation, the electron and radiation energy transport, and the complicated density profiles. Retaining the effects of ablation, density profiles and heat transport all at the same time is so complicated that all the early theories (including mine) of the "ablative" RTI (the RTI of laser accelerated target is commonly addressed as "ablative RTI") only considered each effect separately. This approach has always led to inconsistencies in the theory because the ablation flow depends on the density profile and the latter depends on the heat transport. All the early theories failed to reproduce the results of the experiments and simulations. My colleagues and I, at the Laboratory for Laser Energetics (LLE), recognized that a self-consistent stability analysis had to simultaneously include all three effects. Because the mathematical formulation of the problem became extremely complicated, asymptotic matching techniques had to be used to solve the resulting high-order differential equations. Nevertheless, after about a year of algebraic manipulations, we were able to derive a single formula for the RTI growth rate and understand how the RTI is affected by the ablative convection, finite density gradients and heat transport. We are currently testing the validity of our theory with the results of two-dimensional simulations and are determining which is the "most stable" ablator material.
Figure 2
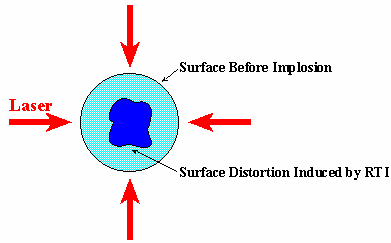
Satisfied with our level of physical understanding concerning the RTI , we are currently involved in developing a technique to suppress the instability. As I showed in my work [Ref. 7], a fast modulation of the laser intensity induces the dynamic stabilization of the RTI. The idea is equivalent to the stabilization of an inverted pendulum by oscillating its base. In laser accelerated targets, a temporal modulation of the laser intensity produces rapid oscillations of the ablation fronts and each Rayleigh-Taylor mode behaves like an inverted pendulum with an oscillating base. Analytical and numerical studies are under way to determined the reduction in the RTI growth caused by the dynamic stabilization.
Representative Publications
- Stability Analysis of Resistive Wall Modes in Rotating Plasmas, Phys. Rev. Lett., Vol.74, p.2949, 1995.
- Destabilization of the Internal Kink by Energetic Circulating Particles, Phys. Rev. Lett., Vol.70, p.3428, 1993.
- Stability of Alfven Gap Modes in Burning Plasmas, Phys. Fluids B, Vol.4, p.1465, 1992.
- The Elliptically-Induced Alfven Eigenmode, Phys. Fluids B, Vol.3, p.1865, 1991.
- Stability Analysis of Ablation Fronts with SmallFroude Numbers, in press: Phys. Plasmas (December 1996).
- Self-Consistent Stability Analysis of Ablation Fronts in ICF, Phys. Plasmas, Vol.3, p.2122, 1996.
- Stability Analysis of Unsteady Ablation Fronts, Phys.Rev. Lett., Vol.71, p.3131, 1993.
Research Interests
- Thermonuclear plasmas
- Controlled thermonuclear fusion
- Magnetic and inertial confinement fusion
- High-energy-density physics
